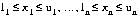
Minimize (or maximize) | c1x1 + c2x2 + . . . + cnxn | ||
subject to | a11x1 + a12x2 + . . . + a1nxn | ~ | b1 |
a21x1 + a22x2 + . . . + a2nxn | ~ | b2 | |
. . . | |||
am1x1 + am2x2 + . . . + amnxn | ~ | bm | |
with these bounds |
| ||
In the most basic linear optimization problem, the variables of the objective function are continuous in the mathematical sense, with no gaps between real values. To solve such linear programming problems, ILOG CPLEX implements optimizers based on the simplex algorithms (both primal and dual simplex) as well as primal-dual logarithmic barrier algorithms. These alternatives are explained more fully in Chapter 4, Solving Linear Programming Problems.
ILOG CPLEX is also a tool for solving linear programming problems in which some or all of the variables must assume integer values in the solution. Such problems are known as mixed integer programs or MIPs because they may combine continuous and discrete (for example, integer) variables in the objective function and constraints. Within the category of mixed integer programs, we distinguish two kinds of discrete integer variables: if the integer values of the discrete variables must be either 0 (zero) or 1 (one), then we refer to them as binary; if the integer values are not restricted in that way, we refer to them as general integer variables. This manual explains more about the separately licensed ILOG CPLEX Mixed Integer Optimizer in Chapter 5, Solving Mixed Integer Programming Problems.
ILOG CPLEX can also handle certain problems in which the objective function is not linear but quadratic. (The constraints in such a problem are still linear.) Such problems are known as quadratic programs or QPs. Chapter 7, Solving Quadratic Programming Problems covers those kinds of problems.
ILOG CPLEX also offers a Network Optimizer aimed at a special class of linear problem with network structures. ILOG CPLEX can optimize such problems as ordinary linear programs, but if ILOG CPLEX can extract all or part of the problem as a network, then ILOG CPLEX will apply its more efficient Network Optimizer to that part of your problem and use the partial solution it finds there to construct an advanced starting point to optimize the rest of the problem. Chapter 6, Solving Network-Flow Problems offers more detail about how the CPLEX Network Optimizer works.