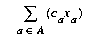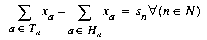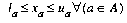A network-flow problem finds the minimal-cost flow through a network, where a network consists of a set N of nodes and a set A of arcs connecting the nodes. An arc a in the set A is an ordered pair (i, j) where i and j are nodes in the set N; node i is called the tail or the from-node and node j is called the head or the to-node of the arc a. Not all the pairs of nodes in a set N are necessarily connected by arcs in the set A. More than one arc may connect a pair of nodes; in other words, a1 = (i, j) and a2 = (i, j) may be two arcs in A, both connecting the nodes i and j in N.
Each arc may be associated with four values:
- xa is the flow value, that is, the amount passing through the arc a from its tail (or from-node) to its head (or to-node). The flow values are the modeling variables of a network-flow problem. Negative values are allowed; a negative flow value indicates that there is flow from the head to the tail.
- la, the lower bound, determines the minimum flow allowed through the arc a. By default, the lower bound on an arc is 0 (zero).
- ua, the upper bound, determines the maximum flow allowed through the arc a. By default, the upper bound on an arc is positive infinity.
- ca, the objective value, determines the contribution to the objective function of one unit of flow through the arc.
Each node is associated with one value:
By convention, a node with strictly positive supply value (that is, sn > 0) is called a supply node or a source, and a node with strictly negative supply value (that is, sn < 0) is called a demand node or a sink. A node where sn = 0 is called a transshipment node. The sum of all supplies must match the sum of all demands; if not, then the network flow problem is infeasible.
Tn is the set of arcs whose tails are node n; Hn is the set of arcs whose heads are node n. The usual form of a network problem looks like this:
That is, for each node, the net flow entering and leaving the node must equal its supply value, and all flow values must be within their bounds. The solution of a network-flow problem is an assignment of flow values to arcs (that is, the modeling variables) to satisfy the problem formulation. A flow that satisfies the constraints and bounds is feasible.