Changing Quadratic Terms

ILOG CPLEX distinguishes between a quadratic algebraic term and a quadratic matrix coefficient. The quadratic algebraic terms are the coefficients that appear in the algebraic expression defined as part of the ILOG CPLEX LP format. The quadratic matrix coefficients appear in Q. The quadratic coefficient of an off-diagonal term must be distributed within the Q matrix, and it is always one-half the value of the quadratic algebraic term.

To clarify that terminology, consider this example:

Minimize a + b + 1/2(a2 + 4ab + 7b2)

subject to a + b 10

with these bounds a 0 and b 0

The off-diagonal quadratic algebraic term in that example is 4, so the quadratic matrix Q is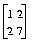

In a QP, you can change the quadratic matrix coefficients in the Interactive Optimizer by using the command change qpterm.
From the Callable Library, use the routine CPXchgqpcoef() to change quadratic matrix coefficients.
Concert Technology does not support direct editing of expressions other than linear expressions. Consequently, to change a quadratic objective function, you need to create an expression with the modified quadratic objective and use IloObjective::setExpr() to install this new expression in the model's objective.

Changing an off-diagonal element changes the corresponding symmetric element as well. In other words, if a call to CPXchgqpcoef() changes Q(i, j) to a value, it also changes Q(j, i) to that same value.

To continue our example, if we want to change the off-diagonal quadratic term from 4 to 6, we would use this sequence of commands in the Interactive Optimizer:

CPLEX> change qpterm
Change which quadratic term [`variable' `variable']: 
a b
Present quadratic term of variable `a', variable `b' 
is 4.000000.
Change quadratic term of variable `a', variable `b' 
to what: 6.0
Quadratic term of variable `a', variable `b' changed 
to 6.000000.

From the Callable Library, the CPXchgqpcoef() call to change the off-diagonal term from 4 to 6 would change both of the off-diagonal matrix coefficients from 2 to 3. Thus, the indices would be 0 and 1, and the new matrix coefficient value would be 3.

If you have entered a linear problem without any quadratic terms, and you want to create quadratic terms, you must first change the problem type to QP. To do so, use the command change problem qp. This command will create an empty quadratic matrix with Q = 0.

When you change quadratic terms, there are still restrictions on the properties of the Q matrix. In a minimization problem, it must be convex, positive semi-definite. In a maximization problem, it must be concave, negative semi-definite. For example, if you change the sense of an objective function in a convex Q matrix from minimization to maximization, you will thus make the problem unsolvable. Likewise, in a convex Q matrix, if you make a term negative, you will thus make the problem unsolvable.