Simulation
Shannon offered a good definition of simulation: "We will define simulation as the process of designing a model of a real system and conducting experiments with this model for the purpose of understanding the behavior of the system and/or evaluating various strategies for the operation of the system.” (Shannon 1998).
These relationships and hypotheses (see note 1) describe the behavior of the system and an experimental environment that represents the target of the study is created. The various relationships and rules, which are usually mathematical (see note 2) or logical, make up the model, the tool that acquires data and provides answers about the system.

Figure 1: Model of the Sagrada Família.
Gordon (1978) establishes a classification of the models shown in the next figure.

Figure 2: Types of models (Gordon 1978)
Because of the structure of the model rules, the way they are implemented and the elements involved, different criteria can be defined to classify simulation models.
In person-to-person simulations, the model is based on individuals that play different roles. Social simulations are one example. The purpose of this kind of study is usually to analyze the reactions of individuals or groups. Job interview training is a more specific example.
Another kind of simulation involves the physical reproduction of a system. Under controlled conditions, a scale model of the system is constructed (Figure 1 shows a physical reproduction of the crypt of the Sagrada Familia temple in Barcelona).
Another kind of simulation is based on person-to-computer models.In these models, a person answers questions posed by a computer.Examples include training through financial strategy games, flight simulators, etc.
Finally, computer simulation models usually do not require user intervention. A computer program (set of decision rules) transforms input and obtains output. The category of computer simulation models can be divided into subcategories based on the set of techniques applied in the construction of the model:
- Monte Carlo simulations: The Monte Carlo method provides approximate solutions to a variety of mathematical problems by performing statistical sampling experiments on a computer. Remarkably, the method applies to problems with absolutely no probabilistic content as well as to those with inherent probabilistic structure (Fishman 1996).
- Continuous simulations: These models are characterized by the representation of the evolution of the variables of interest in a continuous way. In general this method uses ordinary differential equations if a evolution of a characteristic over the time is considered, or partial derivate equations is the evolution over space are considered too (Guasch, Piera et al. 2002).
- Discrete events: In these models, time proceeds in discrete time steps. States variables change its value in no periodic time moments. This moments are related with the event occurrence (Guash, Piera et al. 2002).
- MAS: Multi-agent systems involve a set of intelligent agents. Based on the interaction of these agents, a complex behavior emerges. Agents are fundamentally different from software packages and other commercial programs. They must have special characteristics or attributes (adaptability, mobility, transparency and accountability, ruggedness, slf-starters, user centered) (Murch and Johnson 1999).
Other classifications are presented in the next table depending on different criteria (Guash et al. 2002)
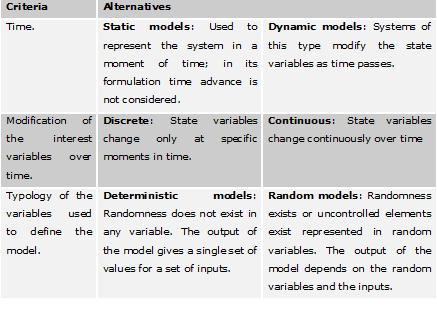
Table 1: Models classification.
Others classifications exists, for instance a classification of the modeling languages in five categories CT, CT+, DE, DE+, and CT/DE where CT means continuous time, DE discrete-event and DT discrete-time, (Beek and Rooda 1998) can be reviewed.
Methodologies based on discrete events (activity scanning, process interaction and, more specifically, event scheduling) allows us to obtain a very accurate level of detail in order to study industrial problems.
However, interest has increasingly focused on the study and analysis of systems with rich behavior that result from the interaction of complex entities and the observation of how these interactions modify the main
modeling process.
Notes:
Simplification hypotheses are not true in the system but are used in the construction of the model to simplify the modeling process (and sometimes just to make this process possible, due to the inherent complexity of the system).
Modeling using differential equations was traditionally one of the most common methodologies for studying different systems. The need for more detail made mathematical models more complex, which made construction difficult in two ways. The first was a modeling problem: there were more differential equations and more relationships between the equations. The second problem related to computing solutions: as the number of differential equations increased, the solution became more difficult and was sometimes impossible.
References
Beek, D.A. van; Rooda, J.E. 1998, Languages and applications in hybrid modelling: positioning of chi, Proc. 9th Symposium on Information Control in Manufacturing, Vol. II, Nancy, 1998, pp. 77-82.
Fishman, George S., 1996, Monte Carlo: Concepts, Algorithms and Applications, Springer, 698 pages, ISBN 038794527X
Gordon, Geoffrey, 1978, System simulation, Ed. Prentice Hall Inc, Englewood Cliffs, New Jersey 07632
Guasch, Antoni; Piera, Miquel Àngel; Casanovas, Josep; Figueres, Jaime. 2002. Modelado y simulación. Aplicación a procesos logísticos de fabricación y servicios. Edicions UPC.
Murch, Richard.; Johnson, Tony. 1999, Intelligent software agents, Prentice Hall PTR, ISBN 0-13-011021-3
Shannon, Robert E. 1998. Introduction to the art and science of simulation, Proceedings of the 1998 Winter Simulation Conference.