Conventionally, a quadratic program (QP) is formulated this way:

Minimize    1/2 xTQx + cTx

subject to   Ax ~ b

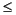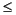with these bounds l  x  u

where the relation ~ may be any combination of equal to, less than or equal to, greater than or equal to, or range constraints. As in other problem formulations, l indicates lower and u upper bounds. Q is a matrix of objective function coefficients. That is, the elements Qjj are the coefficients of the quadratic terms xj2, and the elements Qij and Qji are summed together to be the coefficient of the term xixj.

ILOG CPLEX distinguishes two kinds of Q matrices:

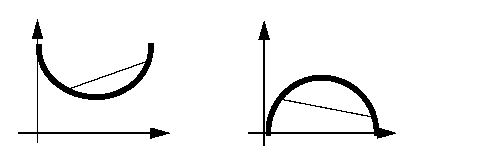
In formal terms, the question of whether a quadratic objective function is convex or concave is equivalent to whether the matrix Q is positive semi-definite or negative semi-definite. For convex QPs, Q must be positive semi-definite; that is, xTQx 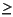 0 for every vector x, whether or not x is feasible. For concave maximization problems, the requirement is that Q must be negative semi-definite; that is, xTQx  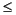0 for every vector x. It is conventional to use the same term, positive semi-definite, abbreviated PSD, for both cases, on the assumption that a maximization problem with a negative semi-definite Q can be transformed into an equivalent PSD.

For a separable function, it is sufficient to check whether the individual diagonal elements of the matrix Q are of the correct sign. For a nonseparable case, it may be less easy to decide in advance the convexity of Q. However, ILOG CPLEX detects this property during the early stages of optimization and terminates if the quadratic objective term in a QP is found to be not PSD.