Discontinuous Piecewise Linear Functions
 PREVIOUS
NEXT
PREVIOUS
NEXT
Discontinuous Piecewise Linear Functions |
INDEX
 PREVIOUS
NEXT
PREVIOUS
NEXT
|
Thus far, you have seen a piecewise linear function where the segments are continuous. Intuitively, in a continuous piecewise linear function, the endpoint of one segment has the same coordinates as the initial point of the next segment, as in Figure 18.1.
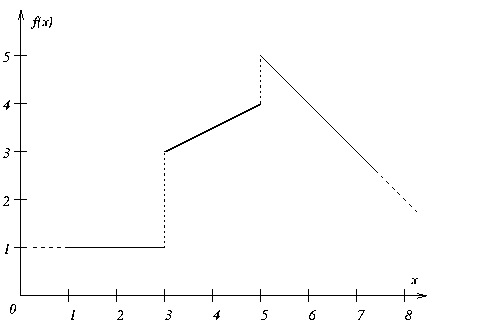
There are piecewise linear functions, however, where the endpoint of one segment and the initial point of the next segment may have the same x coordinate but differ in the value of f(x). Such a difference is known as a step in the piecewise linear function, and such a function is known as discontinuous. Figure 18.2 shows a discontinuous piecewise linear function with two steps.
Syntactically, a step is represented in this way:
By convention, a breakpoint belongs in both segments associated with the step. For example, in Figure 18.2, at the breakpoint x=3, the points (3,1) and (3,3) are both admissible. Similarly, when x = 5, the points (5,4) and (5,5) are both admissible.
However, isolated points, as explained in Isolated Points in Piecewise Linear Functions, are not allowed, neither in continuous nor in discontinuous piecewise linear functions. In fact, only one step is allowed at a given point.
In Concert Technology, a discontinuous piecewise linear function is represented as an instance of the class IloPiecewiseLinear (the same class as used for continuous piecewise linear functions). For example, the function in Figure 18.2 is declared in this way:
IloPiecewiseLinear(x, IloNumArray(env, 4, 3. ,3. ,5. ,5.), IloNumArray(env, 5, 0., 2., 0.5, 1., -1.), 0, 1); |
| Copyright © 1987-2007 ILOG S.A. All rights reserved. Legal terms. | PREVIOUS NEXT |